
Can a procedure call itself?
When a procedure calls for itself this is called recursion. Recursion is almost a fundamental part of any functional programming language these days. The ability to solve problems with recursion has changed the way problems are addressed. Let's take a look at a simple example:
######################################
# Written by Nelson
# Example ch6p19.tcl
# This program offers an example of
# the use of recursion by finding
# the factorial on N
# i.e. f(x)=x!
######################################
####################
# Procedure section
####################
######################################################
# Procedure fact collects 1 variables that the returns
# the results of n! or N Factorial.
######################################################
proc fact {n} {
if {$n<=1} {
return 1
} else {
return [expr $n*[fact [expr $n-1]]]
}
}
######################################################
# Procedure clean will remove old widgets
######################################################
proc clean {} {
if [winfo exists .msg] {destroy .msg}
}
##################################
# The main code section.
##################################
clean
# Try other values for the var value.
set value 8
message .msg -width 15c -text "The factorial of $value is [fact $value]"
pack .msg
Enough already, take off the training wheels!
I think it is a good time to get into some nice mathematically fundamental programs. The below assignments will help you review some of the more basic mathematical operations.
Assignment 6.19
Modify the example ch6p19.tcl to allow the user to enter a number for the
factorial operation.
Assignment 6.20
Modify your answer to Assignment 6.19 to check for the correct type of input.
Consider expr int(arg) and examine: http://www.scriptics.com/man/tcl8.0/TclCmd/expr.htm
Assignment 6.21
Write a program to perform a summation operation. i.e. The summation
of 5 is equal to 5+4+3+2+1=15. Allow the users to input numbers into
the program.
Assignment 6.22
Write a program that will find the midpoint M(xm,ym) of a line segment with
end points P1(x1,y1) and P2(x2,y2). Consider (x1+x2)/2 and (y1+y2)/2.
Assignment 6.23
Write a program what will find the slope M of a line L given 2 points P1(x1,y1)
and P2(x2,y2) on L. Consider rise over run.
Assignment 6.24
Write a program that will accept 2 points P(x,y) and P1(x1,y1) to determine
the slope M and y intercept B of the line that contains P and P1. Consider
the Point-Slope Equation (y-y1)=m(x-x1) and Slope-Intercept Equation
y=mx+b.
Assignment 6.25
Write a program that will accept a point P(x,y) and slope M to determine the
y intercept B of the line containing P. Consider the Slope-Intercept
Equation y=mx+b.
Assignment 6.26
Write a program that will accept 4 points, P(x,y) and P0(x0,y0) elements of
line L1, and P1(x1,y1) and P2(x2,y2) elements of line L2. From these
points determine if the lines L1 and L2 are parallel, perpendicular, or other.
Assignment 6.27
Write a program that will perform the Floor function operation. The
Floor function also known as the Greatest Integer function. An example
would be the floor of 3.25, 3.61, and 3.5 would all be 3. i.e.
It is rounding x downward to the nearest integer value. Tcl/Tk has
many built in functions for math operations. Examine: http://www.scriptics.com/man/tcl8.0/TclCmd/expr.htm
for more information.
Assignment 6.28
The quadratic formula is commonly used in math. The formula is derived
from the quadratic equation ax^2+bx+c. Write a program that will accept
values for a, b and c that will yield the values for x for which ax^2+bx+c=0.
(If you need help, use your browser and a search engine to find more information.)
If pack shows, how does one hide?
######################################
# Written by Nelson
# Example ch6p29.tcl
# Modified Example of ch6p19.tcl
# This program offers an example of
# the use of forget to hide widgets:)
####################################
####################
# Procedure section
####################
######################################################
# Procedure fact collects 1 variables that the returns
# the results of n! or N Factorial.
######################################################
proc fact {n} {
if {$n<=1} {
return 1
} else {
return [expr $n*[fact [expr $n-1]]]
}
}
######################################################
# Procedure clean will remove old widgets
######################################################
proc clean {} {
if [winfo exists .msg] {destroy .msg}
if [winfo exists .ent1] {destroy .ent1}
if [winfo exists .but1] {destroy .but1}
if [winfo exists .but2] {destroy .but2}
}
##################################
# The main code section.
##################################
clean
set showMe true
entry .ent1 -textvariable value
message .msg -width 15c -text "First Run"
button .but1 -text Factorial -command {
.msg configure -text " The factorial of $value is [fact $value]
"
}
button .but2 -text "Push Me!" -command {
if {$showMe} {
set showMe false
pack forget .msg
} else {
set showMe true
pack .msg}
}
pack .but1 .msg .ent1 .but2
# Place the widgets.
place .msg -x 20 -y 20
place .ent1 -x 20 -y 50
place .but1 -x 20 -y 80
place .but2 -x 20 -y 110
Assignment 6.29
Write a program that will calculate the area of a triangle, rectangle, cylinder,
cube and a circle. Make these choices available via a radiobutton for
each choice. Also use labels to offer the correct descriptions for
your entry widgets. Hide unnecessary widgets!
Pick a number, any number.
Selecting a number from a set of numbers with out bias has been a quest of mathematicians for a long time. This number that is selected from a given set is said to be random if in fact the number is selected without bias. Consider the example of a coin being flipped, if the coin always comes up heads then one would want to examine the coins properties. Could it be a two headed coin? A coin that had an equal chance of showing tails as well as heads would be considered to be random in its outcome. Consider a die that always shows the face value of 2 when rolled. Could it be a loaded die. A die that had an equal chance of showing a face value from 1 to 6 would be considered to be random in its outcome. Consider the lottery, if it always came up with the same numbers or even if a single number is always selected, do you think there would be more winners? The idea of using random numbers is actually widely used and with the invention of the computer using random numbers has never been easier. In Tcl/Tk the expr is again our work horse. The random number operation is part of the expr command. Let's take a look at an example:
######################################
# Written by Nelson
# Example ch6p30.tcl
# This program offers an example of
# random numbers.
######################################
####################
# Procedure section
####################
######################################################
# Procedure clean will remove old widgets
######################################################
proc clean {} {
if [winfo exists .l1] {destroy .l1}
if [winfo exists .l2] {destroy .l2}
if [winfo exists .b1] {destroy .b1}
}
##################################
# The main code section.
##################################
clean
label .l1 -text "Random Number"
label .l2 -text " No Number Yet "
button .b1 -text "Get a random number!" -command {
.l2 configure -text [expr rand()]
.b1 configure -text "Get A New Number!"}
pack .l1 .l2 .b1
Here are some screen shots:


Assignment 6.30
Write a program that will emulate a coin toss by offering output of heads
or tails based on a generated random number. (Use labels in this problem.)
Assignment 6.31
Write a program that will emulate a die roll by offering output of a value
from 1 to 6 to represent each face of the die based on a generated random
number. (Use labels in this problem.)
Assignment 6.32
Modify Assignment 6.30 to toss the coin 100 times then count the occurrence
of either heads or tails. (Use labels in this problem.)
Assignment 6.33
Modify the Assignment 6.31 to roll the die 100 times then count the occurrence
of each face. (Use labels in this problem.)
Assignment 6.34
Modify Assignment 6.32 and Assignment 6.33 to allow the user to input the
number of tosses and rolls (respectively) then count occurrences. (Use
labels in this problem.)
Assignment 6.35
Write a program that will emulate a lottery.
After you have completed the above assignment set, you should start to have some insight to what is called probability. Probability deals with the chances that something will occur. In fact, there is an entire branch of mathematics called Statistics that deals with these issues. By utilizing statistics you can predict (with error) the probability that something will occur. Think about how an insurance company knows what premium to charge for different types of automobiles. Consider, as well, how companies know the failure rate of different types of products. What about how they can make the product a good product with a limited life span and the warranties they offer for it. For more information about statistics and probability look for these terms on the internet from your favorite search engine. How do you think statistics and probability is at work in your everyday life?
Assignment 6.36
Write a program that will emulate a game of chance called craps. The
game uses 2 dice.. The rules are as follows:
1.) On the first roll if the sum of the dice is 7 or 11 the player wins.
2.) If the sum of the 2 dice is 2, 3, or 12 on the first roll the player
loses.
3.) If the sum of the 2 dice is 4, 5, 6, 8, 9, or 10 on the first throw,
this sum becomes the point.
4.) To win, if a point has been set, the player must roll the point.
If you roll a 7 with the point set the player loses.
Think about the probability of each number that is rolled.
Array of sunshine can brighten your day.
Arrays in Tcl are sometimes called associative arrays. The main difference between arrays in other programming languages and Tcl is that other languages require an integer for the element name (index). An array in Tcl will take names for an element name hence the association. Consider the following concept:
set auto(spare) "Full Size"
set auto(miles) "30,000"
set auto(doors) 2
However, in other programming languages you would have had to use an integers to represent spare, miles and doors. There are several means to work with arrays in Tcl so I encourage you to examine the manual pages on this topic. Below is a simple example that you should be able to see how to create an array, seed it with values, return a value from a given element name (index), list the element names (indexes) and determine the size of the array :
###########################
## Example Code by Nelson
## for arrays arrayExample.tcl
###########################
###### Procedure Scetion###
proc {f_x} {x} {
##############
# Operation: Squares a number.
# Collects : variable called x
# Returns : Returns the math operation x*x
##############
return [expr $x*$x]
}
# Close f_x
## End Procedure Section ##
#### Main Code Section ####
set tempString ""
for {set z 0} {$z<10} { incr z} {
set arrayName($z) [f_x $z]
set tempString "$tempString, $arrayName($z)"
}
label .l1 -text "Values: $tempString"
label .l2 -text "Values: $arrayName(7)"
label .l3 -text "Array Names:[array names arrayName]"
label .l4 -text "Array Size [array size arrayName]"
pack .l1 .l2 .l3 .l4
Something I will point out is that the list returned from array names has
no particular order.
Prime the engine before you turn the key!
The time has come to talk about a special type of integer numbers called primes. By definition, a number is prime if it is evenly divisible by the numbers 1 and itself (no remainder). At first glance one might not see the importance of these special numbers, however, prime numbers are very important. In fact they are the base factors that compose all other integer numbers. Think about some other purposes for prime numbers.
Assignment 6.37
Write a program that will collect a number from the user and determine if
the number is prime. Think about how to test to see if the number is
prime.
Assignment 6.38
Write a program that will find prime numbers in a given range that the user
can input. Then display the numbers found to be prime back to the user
as output. Use arrays to help in the testing and keep a list of prime
numbers. (Hint: write the code to test numbers from 3 to 100 at first.)
Assignment 6.39
Write a program that will output the factor tree of a number entered by the
user to a message widget.
I think I would understand better if I could see the graph.
Graphing is an excellent tool to understand what is occurring within a given situation. Fortunate for Tcl/Tk users there is an extension called the BLT ( http://www.tcltk.com/blt/index.html ) that does wonderful graphs as well as an assortment of other neat operations. We are going to use the BLT to examine some basic mathematical operations and concepts. There are many parts to this extension of Tcl/Tk and only a few examples will be discussed in this workbook. You may want to examine some resources on the internet to find out more information about BLT and any other extension that catches your eye. Graphing will allow us to discuss many excellent mathematical concepts, but first we must get some of the basics of the BLT extension. Take a look at the following example:
# Example for getting started with BLT
# Written by Nelson example blt1.tcl
# get the package
package require BLT
# Check to make sure we are using a later version
if { $tcl_version >= 8.0 } {
namespace import blt::*
namespace import -force blt::tile::*
}
# Create the graph with a title
graph .g1 -title "Nelson Graph"
pack .g1
# Let's use some of the built in functions!
Blt_ZoomStack .g1
Blt_Crosshairs .g1
Blt_ActiveLegend .g1
Blt_ClosestPoint .g1
# Seed the data the way we want
for { set x .1 } { $x <= 3} { set x [expr $x+.05]} {
lappend xVar $x
lappend yVar [expr $x*$x]
lappend zVar [expr $x+1]
}
# Create the graph elements with some options.
.g1 element create "e1" -label "x" -xdata $xVar -ydata $yVar -pixels 1m
.g1 element create "e2" -label "z" -color red -xdata $xVar -ydata $zVar -pixels
.5m
Assignment 6.40
Modify the example blt1.tcl to have 2 additional elements that would represent
the functions f(x)=1/x and f(x)=|x| for values from .1 to 2, with the user
selecting the increments via an entry widget. Make the 2 new elements
yellow and green respectively.
Stay in the shade to avoid a heatstroke!
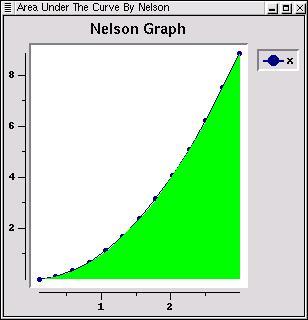
Shading is a wonderful concept when viewing graphs. The BLT allows us to do this. Examine the following example:
#############################
# Example written by Nelson
# blt2.tcl
# Show shading in blt
#############################
package require BLT
if { $tcl_version >= 8.0 } {
namespace import blt::*
namespace import -force blt::tile::*
}
# Set some global vars to keep things clean
set xVar ""
set yVar ""
##############
# Procedure section
##############
# Set values in graph element
##############
proc seeder {step} {
global xVar yVar
if {$step==""} {set step 1}
for { set x .1 } { $x <= 3} { set x [expr $x+ $step]} {
lappend xVar $x
lappend yVar [expr $x*$x]
}
}
entry .e1 -textvar eVar
button .b1 -text "Graph Me" -command {
if [winfo exists .t2] {destroy .t2
set xVar ""
set yVar ""
}
toplevel .t2
wm geometry .t2 300x300+220+100
wm title .t2 "Area Under The Curve By Nelson"
graph .t2.g1 -title "Nelson Graph"
Blt_ZoomStack .t2.g1
Blt_Crosshairs .t2.g1
Blt_ActiveLegend .t2.g1
Blt_ClosestPoint .t2.g1
seeder $eVar
.t2.g1 element create "e1" -label "x" -xdata $xVar -ydata $yVar -pixels
1m
.t2.g1 marker create polygon -coords "1 0 [.t2.g1 element cget e1 -data]
3 0" -fill green
pack .t2.g1
}
pack .b1 .e1
Here are some screen shots:
Assignment 6.41
The example blt2.tcl has some interesting operations placed in the code.
Write an explanation for each line of code in the program. Explain
what you think each line does in detail. After you have completed this
assignment, type in the following code and modify some of its operations to
better understand the example.
Should you limit the amount of cartoons you watch?
I would think not, however, this might help you better understand what we are going to discuss next which is limits. The concept of the limit is another commonly used mathematical operation. The idea of the limit is to examine points very close to a given point x, to ascertain an idea of what is going to happen at f(x). The idea has been introduced, you can now grapple with the idea. If you would like a formal definition of the limit, try using your favorite search engine or ask your instructor for the definition and some examples.
Assignment 6.42
Write a program that will examine the graph of f(x)=1/x for values very small
but not equal to 0.
How can I find area under a curve?
Finding area under a curve is an excellent subject to discuss at this time. You should have all the tools to perform an examination of area under a curve. Think about how you find area in general. Now let's talk about how we find area in say a rectangle. The common formula is LxW which will yield the area but a rectangle doesn't fit a curve. (Or does it?)
Assignment 6.43
Consider how you could modify the LxW formula to find area under a curve.
Also consider the error involved in using these estimations. Explain
your ideas and concepts in detail.
Assignment 6.44
Write a program that will estimate area under a curve. (You should be
able to accept input to make the estimation more precise.)